Exploratory adaptation in cellular networks
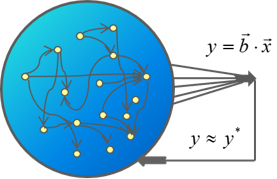 Cells have multiple gene-regulation “programs” to answer to specific challenges; still, they are sometimes required to address unforeseen challenges for which no response is readily available. Here, exploratory dynamics can provide an in-principle unlimited repertoire of new responses and cell states; this process is, in some respects, similar to learning. We study exploratory adaptation in theoretical models of random networks, with particular focus on properties of biological networks that allow such exploration in high dimensional space to converge. [Schreier, Soen & Brenner 2017]
Cells have multiple gene-regulation “programs” to answer to specific challenges; still, they are sometimes required to address unforeseen challenges for which no response is readily available. Here, exploratory dynamics can provide an in-principle unlimited repertoire of new responses and cell states; this process is, in some respects, similar to learning. We study exploratory adaptation in theoretical models of random networks, with particular focus on properties of biological networks that allow such exploration in high dimensional space to converge. [Schreier, Soen & Brenner 2017]
 The experimental roots of this theory come from a joint work with Erez Braun from the Physics Dept. at Technion. Yeast cells were rewired synthetically and conditions are set such that the genetic regulatory system faces unforeseen severely challenging conditions. We have found that rewired cells can adapt over short (~10 generation) timescales to these challenging conditions. This adaptation is not induced by random mutation but is nevertheless stable over hundreds of generations. We studied the roles of population phenotypic variability, global gene expression and other cellular mechanisms on this plastic behavior, which we believe are representative of the physiological plasticity exhibited in evolution following gene co-option events. [Stolovicki et al., 2006 ; Stern, et al., 2007]
The experimental roots of this theory come from a joint work with Erez Braun from the Physics Dept. at Technion. Yeast cells were rewired synthetically and conditions are set such that the genetic regulatory system faces unforeseen severely challenging conditions. We have found that rewired cells can adapt over short (~10 generation) timescales to these challenging conditions. This adaptation is not induced by random mutation but is nevertheless stable over hundreds of generations. We studied the roles of population phenotypic variability, global gene expression and other cellular mechanisms on this plastic behavior, which we believe are representative of the physiological plasticity exhibited in evolution following gene co-option events. [Stolovicki et al., 2006 ; Stern, et al., 2007]
Phenotypic Variability in Cell Populations
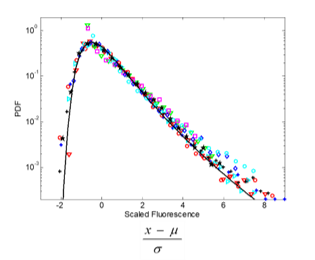 Variation is a fundamental property of biological populations at all levels. In particular highly expressed proteins are usually relevant phenotypes that nevertheless exhibits large variation among cells in a clonal population under uniform conditions. We study protein distributions in microorganism populations using Statistical Mechanics approaches and concepts, via an experiment-theory collaboration (with Erez Braun, Technion; Hanna Salman, Pittsburgh Universaity). We have characterized the quantitative features of protein distributions in dividing cell populations: these are highly non-Gaussian and skewed. We have found that these protein distributions from two microorganisms, yeast and bacteria, and under a broad range of conditions, collapse to a universal curve under scaling. Moreover the protein temporal fluctuations in the same scaled units obey an ergodic property and display the same distribution shape as the population snapshots. This universality indicates a strong buffering of the measured phenotypes from microscopic processes.[Salman et al.,
Variation is a fundamental property of biological populations at all levels. In particular highly expressed proteins are usually relevant phenotypes that nevertheless exhibits large variation among cells in a clonal population under uniform conditions. We study protein distributions in microorganism populations using Statistical Mechanics approaches and concepts, via an experiment-theory collaboration (with Erez Braun, Technion; Hanna Salman, Pittsburgh Universaity). We have characterized the quantitative features of protein distributions in dividing cell populations: these are highly non-Gaussian and skewed. We have found that these protein distributions from two microorganisms, yeast and bacteria, and under a broad range of conditions, collapse to a universal curve under scaling. Moreover the protein temporal fluctuations in the same scaled units obey an ergodic property and display the same distribution shape as the population snapshots. This universality indicates a strong buffering of the measured phenotypes from microscopic processes.[Salman et al., 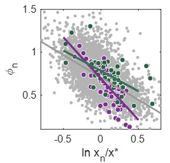 2012 ; Brenner et al., 2015]
2012 ; Brenner et al., 2015]
The empirical results on universality and buffering suggests viewing and modeling protein variability at a mesoscopic scale. We find that a simple model captures the universal distribution shape, and applies both to protein content and to cell size. However, the dynamic process described by this model is itself variable among single cells! Growth homeostasis is implemented at variable strength in individual bacteria. [Brenner et al., 2015; Susman et al., 2018 ]
Variability and dynamics of synapse populations
 Populations of synapses have long been thought to be important in learning and memory. However only recently have quantitative measurements of large populations of synapses become directly accessible. In collaboration with the lab of Noam Ziv at the Technion, we study and model both statistical and dynamical properties of such synaptic populations. We have found that many properties of these populations can be captured by a mesoscopic-scale effective model known as the Kesten Process. At the biophysical level we have found that cooperative binding and unbinding are sufficient and necessary conditions to recover the statistical properties of synaptic populations. [Statman et al., 2014; Shomar et al., 2017; Ziv & Brenner, 2018]
Populations of synapses have long been thought to be important in learning and memory. However only recently have quantitative measurements of large populations of synapses become directly accessible. In collaboration with the lab of Noam Ziv at the Technion, we study and model both statistical and dynamical properties of such synaptic populations. We have found that many properties of these populations can be captured by a mesoscopic-scale effective model known as the Kesten Process. At the biophysical level we have found that cooperative binding and unbinding are sufficient and necessary conditions to recover the statistical properties of synaptic populations. [Statman et al., 2014; Shomar et al., 2017; Ziv & Brenner, 2018]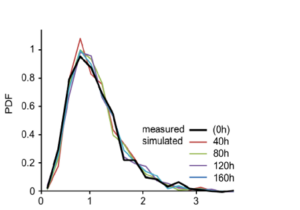
Cooperative interactions between microorganisms
Cells (and microorganisms in particular) interact with one another by direct signaling as well as indirectly through their common environment. These interactions are mediated by products of cell metabolism and gene expression. We are interested in the relation between these two levels of organization; namely in the effects of cellular processes, through interactions, on the population-level dynamics and back on the cells. Game theory and nonlinear dynamics systems are the main tools we use in this research. Our recent work focuses on the dramatic effects of fluctuations on these systems, showing that coexistence can be induced purely by such fluctuations. [Behar et al.,2015; Behar et al., 2016; Elhanati, Schuster & Brenner,2011; Schuster et al., 2010]
Adaptive cellular response to signals
Cells sense their environment and respond to it adaptively. These adaptive responses address the challenge of environments changing over an extremely broad range of time and signal scales. We study adaptive cellular response in a general theoretic framework which can distinguish universal features common to many cellular systems, from system-specific ones. In particular we address kinetic mechanisms underlying dynamic-range enlargement (background compensation) and multiple-time-scale behavior. [Friedlander & Brenner, 2011; Friedlander & Brenner, 2009; Gilboa, Chen & Brenner, 2005]
